Exponential distribution

Exponential
Probability density function
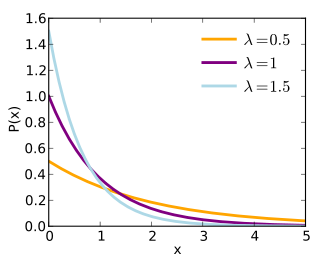
Cumulative distribution function
Parameters	λ > 0 rate, or inverse scale
Support	x ∈ [0, ∞)
PDF	λ e^−λx
CDF	1 − e^−λx
Quantile	−ln(1 − F) / λ
Mean	λ⁻¹ (= β)
Median	λ⁻¹ ln(2)
Mode	0
Variance	λ⁻² (= β²)
Skewness	2
Ex. kurtosis	6
Entropy	1 − ln(λ)
MGF	${\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda$ $\frac{\lambda}{\lambda-t}, \text{ for } t < \lambda$
CF	${\frac {\lambda }{\lambda -it}}$ $\frac{\lambda}{\lambda-it}$
Fisher information	$\lambda ^{-2}$ $\lambda^{-2}$

In probability theory and statistics, the exponential distribution (a.k.a. negative exponential distribution) is the probability distribution that describes the time between events in a Poisson process, i.e. a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson processes, it is found in various other contexts.

The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.

The exponential distribution is used to model the time between the occurrence of events in an interval of time, or the distance between events in space. The exponential distribution may be useful to model events such as

The exponential distribution is an appropriate model if the following conditions are true.

If these conditions are true, then X is an exponential random variable, and the distribution of X is an exponential distribution. If these conditions are not true, then the exponential distribution is not appropriate. Alternative distributions such as the Weibull or gamma may give a better fit to the data, or a semi-parametric model, such as the Cox proportional-hazards model, may be required for statistical analysis.

...
Wikipedia