Gamma distribution
Probability density function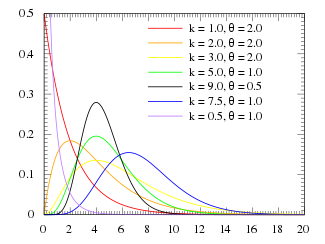
|
||
Cumulative distribution function
|
||
| Parameters | ||
|---|---|---|
| Support | ||
| CDF | ||
| Mean |
(see digamma function) |
(see digamma function) |
| Median | No simple closed form | No simple closed form |
| Mode | ||
| Variance |
(see trigamma function) |
(see trigamma function) |
| Skewness | ||
| Excess kurtosis | ||
| Entropy | ||
| MGF | ||
| CF | ||
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The common exponential distribution and chi-squared distribution are special cases of the gamma distribution. There are three different parametrizations in common use:
In each of these three forms, both parameters are positive real numbers.
The gamma distribution is the maximum entropy probability distribution for a random variable X for which E[X] = kθ = α/β is fixed and greater than zero, and E[ln(X)] = ψ(k) + ln(θ) = ψ(α) − ln(β) is fixed (ψ is the digamma function).
The parameterization with k and θ appears to be more common in econometrics and certain other applied fields, where e.g. the gamma distribution is frequently used to model waiting times. For instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution.
The parameterization with α and β is more common in Bayesian statistics, where the gamma distribution is used as a conjugate prior distribution for various types of inverse scale (aka rate) parameters, such as the λ of an exponential distribution or a Poisson distribution – or for that matter, the β of the gamma distribution itself. (The closely related inverse gamma distribution is used as a conjugate prior for scale parameters, such as the variance of a normal distribution.)
...
Wikipedia






![\scriptstyle \mathbf {E} [X]=k\theta](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5a8d3180543b0fefb41ad099eb647b140c928e7)
![\scriptstyle \mathbf {E} [\ln X]=\psi (k)+\ln(\theta )](https://wikimedia.org/api/rest_v1/media/math/render/svg/88bfb2a2be186941b62da93c01e02f1861e5101e)
![\scriptstyle \mathbf {E} [X]={\frac {\alpha }{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fdd98d6e7948ccb700bc1abf7aa5281b83e2b48)
![\scriptstyle \mathbf {E} [\ln X]=\psi (\alpha )-\ln(\beta )](https://wikimedia.org/api/rest_v1/media/math/render/svg/770287e8b2ca056d0bba7dd27de11baf5d538be8)


![\scriptstyle\operatorname{Var}[ X] = k \theta^2](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a1ec4e223012e3ee6f082c633097236cfd8e626)
![\scriptstyle\operatorname{Var}[\ln X] = \psi_1(k)](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bfbfe7e400c828ffdfca5c07ea446418273faaa)
![\scriptstyle \operatorname{Var}[ X] = \frac{\alpha}{\beta^2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/813af21e82fb565bbb8094e9c68e351af5b96b7c)
![\scriptstyle\operatorname{Var}[\ln X] = \psi_1(\alpha)](https://wikimedia.org/api/rest_v1/media/math/render/svg/badd9264fafaa1c825f8839923fe5e1423dd2aa2)




![\scriptstyle \begin{align}
\scriptstyle k &\scriptstyle \,+\, \ln\theta \,+\, \ln[\Gamma(k)]\\
\scriptstyle &\scriptstyle \,+\, (1 \,-\, k)\psi(k)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d2c89d9e0f1b9542b044217fab69ab3de01add)
![\scriptstyle \begin{align}
\scriptstyle \alpha &\scriptstyle \,-\, \ln \beta \,+\, \ln[\Gamma(\alpha)]\\
\scriptstyle &\scriptstyle \,+\, (1 \,-\, \alpha)\psi(\alpha)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/396dc40c039037452184e1312d82a4b76399dbb7)



