Weibull distribution

Weibull (2-Parameter)
Probability density function
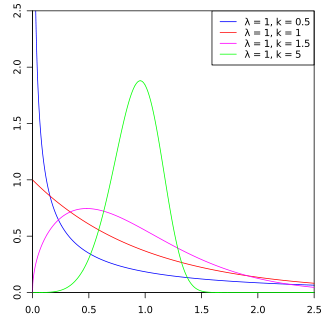
Cumulative distribution function
Parameters	$\lambda \in (0,+\infty )\,$ $\lambda\in (0, +\infty)\,$ scale $k\in (0,+\infty )\,$ $k\in (0, +\infty)\,$ shape
Support	$x\in [0,+\infty )\,$ $x \in [0, +\infty)\,$
PDF	$f(x)={\begin{cases}{\frac {k}{\lambda }}\left({\frac {x}{\lambda }}\right)^{k-1}e^{-(x/\lambda )^{k}}&x\geq 0\\0&x<0\end{cases}}$ $f(x)=\begin{cases} \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^{k}} & x\geq0\\ 0 & x<0\end{cases}$
CDF	${\begin{cases}1-e^{-(x/\lambda )^{k}}&x\geq 0\\0&x<0\end{cases}}$ $\begin{cases}1- e^{-(x/\lambda)^k} & x\geq0\\ 0 & x<0\end{cases}$
Mean	$\lambda \,\Gamma (1+1/k)\,$ $\lambda \, \Gamma(1+1/k)\,$
Median	$\lambda (\ln(2))^{1/k}\,$ $\lambda(\ln(2))^{1/k}\,$
Mode	${\begin{cases}\lambda \left({\frac {k-1}{k}}\right)^{\frac {1}{k}}\,&k>1\\0&k\leq 1\end{cases}}$ ${\begin{cases}\lambda \left({\frac {k-1}{k}}\right)^{\frac {1}{k}}\,&k>1\\0&k\leq 1\end{cases}}$
Variance	$\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k}}\right)-\left(\Gamma \left(1+{\frac {1}{k}}\right)\right)^{2}\right]\,$ $\lambda^2\left[\Gamma\left(1+\frac{2}{k}\right) - \left(\Gamma\left(1+\frac{1}{k}\right)\right)^2\right]\,$
Skewness	${\frac {\Gamma (1+3/k)\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}$ $\frac{\Gamma(1+3/k)\lambda^3-3\mu\sigma^2-\mu^3}{\sigma^3}$
Ex. kurtosis	(see text)
Entropy	$\gamma (1-1/k)+\ln(\lambda /k)+1\,$ $\gamma(1-1/k)+\ln(\lambda/k)+1 \,$
MGF	$\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n}}{n!}}\Gamma (1+n/k),\ k\geq 1$ $\sum_{n=0}^\infty \frac{t^n\lambda^n}{n!}\Gamma(1+n/k), \ k\geq1$
CF	$\sum _{n=0}^{\infty }{\frac {(it)^{n}\lambda ^{n}}{n!}}\Gamma (1+n/k)$ $\sum_{n=0}^\infty \frac{(it)^n\lambda^n}{n!}\Gamma(1+n/k)$

In probability theory and statistics, the Weibull distribution /ˈveɪbʊl/ is a continuous probability distribution. It is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Fréchet (1927) and first applied by Rosin & Rammler (1933) to describe a particle size distribution.

The probability density function of a Weibull random variable is:

where k > 0 is the shape parameter and λ > 0 is the scale parameter of the distribution. Its complementary cumulative distribution function is a stretched exponential function. The Weibull distribution is related to a number of other probability distributions; in particular, it interpolates between the exponential distribution (k = 1) and the Rayleigh distribution (k = 2 and $\lambda ={\sqrt {2}}\sigma$ $\lambda = \sqrt{2}\sigma$ ).

...
Wikipedia