Odd graph

Odd graph
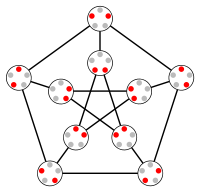
O3 = KG5,2 is the Petersen graph
Vertices	${\displaystyle {\tbinom {2n-1}{n-1}}}$
Edges	${\displaystyle n{\tbinom {2n-1}{n-1}}/2}$
Diameter	n − 1
Girth	3 if n = 2 5 if n = 3 6 if n > 3
Properties	Distance-transitive
Notation	On

In the mathematical field of graph theory, the odd graphs O_n are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.

The odd graph O_n has one vertex for each of the (n − 1)-element subsets of a (2n − 1)-element set. Two vertices are connected by an edge if and only if the corresponding subsets are disjoint. That is, O_n is a Kneser graph KG(2n − 1,n − 1).

O₂ is a triangle, while O₃ is the familiar Petersen graph.

The generalized odd graphs include the odd graphs and the folded cube graphs, and are defined as distance-regular graphs with diameter n − 1 and odd girth 2n − 1 for some n.

Although the Petersen graph has been known since 1898, its definition as an odd graph dates to the work of Kowalewski (1917), who also studied the odd graph O₄. Odd graphs have been studied for their applications in chemical graph theory, in modeling the shifts of carbonium ions. They have also been proposed as a network topology in parallel computing.

The notation O_n for these graphs was introduced by Norman Biggs in 1972. Biggs and Tony Gardiner explain the name of odd graphs in an unpublished manuscript from 1974: each edge of an odd graph can be assigned the unique element of X which is the "", i.e., not a member of either subset associated with the vertices incident to that edge.