Folded cube graph

Folded cube graph
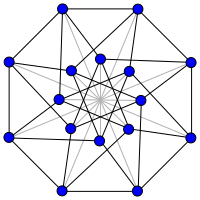
The order-5 folded cube graph (i.e, the Clebsch graph).
Vertices	2n−1
Edges	2n−2n
Diameter	floor(n/2)
Chromatic number	2 (for even n), or 4 (when odd).
Properties	Regular graph Hamiltonian Distance-transitive.

In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.

The folded cube graph of order k (containing 2^k − 1 vertices) may be formed by adding edges between opposite pairs of vertices in a hypercube graph of order k − 1. (In a hypercube with 2ⁿ vertices, a pair of vertices are opposite if the shortest path between them has length n.) It can, equivalently, be formed from a hypercube graph (also) of order k, which has twice as many vertices, by identifying together (or contracting) every opposite pair of vertices.

An order-k folded cube graph is k-regular with 2^k − 1 vertices and 2^k − 2k edges.

The chromatic number of the order-k folded cube graph is two when k is even (that is, in this case, the graph is bipartite) and four when k is odd. The odd girth of a folded cube of odd order is k, so for odd k greater than three the folded cube graphs provide a class of triangle-free graphs with chromatic number four and arbitrarily large odd girth. As a distance-regular graph with odd girth k and diameter (k − 1)/2, the folded cubes of odd order are examples of generalized odd graphs.

When k is odd, the bipartite double cover of the order-k folded cube is the order-k cube from which it was formed. However, when k is even, the order-k cube is a double cover but not the bipartite double cover. In this case, the folded cube is itself already bipartite. Folded cube graphs inherit from their hypercube subgraphs the property of having a Hamiltonian cycle, and from the hypercubes that double cover them the property of being a distance-transitive graph.