Huzita–Hatori axioms
The Huzita–Hatori axioms or Huzita–Justin axioms are a set of rules related to the mathematical principles of paper folding, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane (i.e. a perfect piece of paper), and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.
The axioms were first discovered by Jacques Justin in 1986. Axioms 1 through 6 were rediscovered by Japanese-Italian mathematician Humiaki Huzita and reported at the First International Conference on Origami in Education and Therapy in 1991. Axioms 1 though 5 were rediscovered by Auckly and Cleveland in 1995. Axiom 7 was rediscovered by Koshiro Hatori in 2001; Robert J. Lang also found axiom 7.
The first 6 axioms are known as Huzita's axioms. Axiom 7 was discovered by Koshiro Hatori. Jacques Justin and Robert J. Lang also found axiom 7. The axioms are as follows:
Axiom 5 may have 0, 1, or 2 solutions, while Axiom 6 may have 0, 1, 2, or 3 solutions. In this way, the resulting geometries of origami are stronger than the geometries of compass and straightedge, where the maximum number of solutions an axiom has is 2. Thus compass and straightedge geometry solves second-degree equations, while origami geometry, or origametry, can solve third-degree equations, and solve problems such as angle trisection and doubling of the cube. The construction of the fold guaranteed by Axiom 6 requires "sliding" the paper, or neusis, which is not allowed in classical compass and straightedge constructions. Use of neusis together with a compass and straightedge does allow trisection of an arbitrary angle.
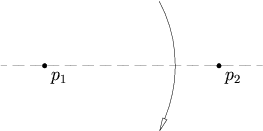
Given two points p1 and p2, there is a unique fold that passes through both of them.
...
Wikipedia