Fundamental theorem on homomorphisms

In abstract algebra, the fundamental theorem on homomorphisms, also known as the fundamental homomorphism theorem, relates the structure of two objects between which a homomorphism is given, and of the kernel and image of the homomorphism.

The homomorphism theorem is used to prove the isomorphism theorems.

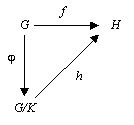
Given two groups G and H and a group homomorphism f : G→H, let K be a normal subgroup in G and φ the natural surjective homomorphism G→G/K (where G/K is a quotient group). If K is a subset of ker(f) then there exists a unique homomorphism h:G/K→H such that f = h φ.

In other words, the natural projection φ is universal among homomorphisms on G that map K to the identity element.

The situation is described by the following commutative diagram:

By setting K = ker(f) we immediately get the first isomorphism theorem.

Similar theorems are valid for monoids, vector spaces, modules, and rings.

...
Wikipedia