Exponentially distributed

Exponential

Probability density function
Cumulative distribution function
Parameters	λ > 0 rate, or inverse scale
Support	x ∈ [0, ∞)
PDF	λ e−λx
CDF	1 − e−λx
Quantile	−ln(1 − F) / λ
Mean	λ−1 (= β)
Median	λ−1 ln(2)
Mode	0
Variance	λ−2 (= β2)
Skewness	2
Ex. kurtosis	6
Entropy	1 − ln(λ)
MGF	${\displaystyle {\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda }$
CF	${\displaystyle {\frac {\lambda }{\lambda -it}}}$
Fisher information	${\displaystyle \lambda ^{-2}}$

In probability theory and statistics, the exponential distribution (a.k.a. negative exponential distribution) is the probability distribution that describes the time between events in a Poisson process, i.e. a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson processes, it is found in various other contexts.

The exponential distribution is not the same as the class of exponential families of distributions, which is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes the normal distribution, binomial distribution, gamma distribution, Poisson, and many others.

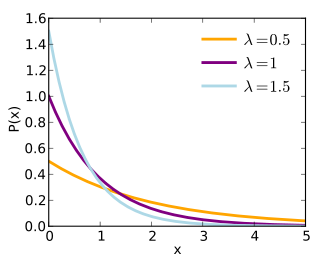
The probability density function (pdf) of an exponential distribution is

Alternatively, this can be defined using the right-continuous Heaviside step function, H(x) where H(0)=1:

Here λ > 0 is the parameter of the distribution, often called the rate parameter. The distribution is supported on the interval [0, ∞). If a random variable X has this distribution, we write X ~ Exp(λ).

The exponential distribution exhibits infinite divisibility.

The cumulative distribution function is given by