Snub disphenoid

Snub disphenoid
Type	Johnson J83 - J84 - J85
Faces	4+8 triangles
Edges	18
Vertices	8
Vertex configuration	4(34) 4(35)
Symmetry group	D2d
Dual polyhedron	-
Properties	convex, deltahedron
Net

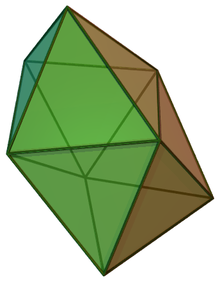
In geometry, the snub disphenoid, Siamese dodecahedron, or dodecadeltahedron is a three-dimensional convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight deltahedra (convex polyhedra with equilateral triangle faces) and one of the 92 Johnson solids (non-uniform convex polyhedra with regular faces).

This shape was called a Siamese dodecahedron in the paper by Hans Freudenthal and B. L. van der Waerden (1947) which first described the set of eight convex deltahedra. There are other simplicial dodecahedra, such as the hexagonal bipyramid, but this is the only one that can be realized with equilateral faces.

The dodecadeltahedron name was given to this shape by Bernal (1964), referring to the fact that it is a 12-sided deltahedron. Bernal was interested in the shapes of holes left in irregular close-packed arrangements of spheres, so he used a restrictive definition of deltahedra, in which a deltahedron is a convex polyhedron with triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. This restrictive definition disallows the triangular bipyramid (as forming two tetrahedral holes rather than a single hole), pentagonal bipyramid (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and icosahedron (because it has interior room for another sphere). Bernal writes that the snub disphenoid is "a very common coordination for the calcium ion in crystallography".

...
Wikipedia