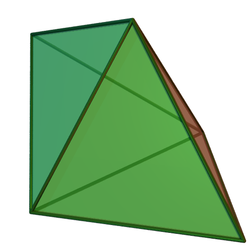
Triangular bipyramid
| Triangular bipyramid | |
|---|---|
 |
|
| Type |
Bipyramid and Johnson J11 - J12 - J13 |
| Faces | 6 triangles |
| Edges | 9 |
| Vertices | 5 |
| Schläfli symbol | { } + {3} |
| Coxeter diagram | |
| Symmetry group | D3h, [3,2], (*223) order 12 |
| Rotation group | D3, [3,2]+, (223), order 6 |
| Dual polyhedron | Triangular prism |
| Face configuration | V3.4.4 |
| Properties | Convex, face-transitive |
In geometry, the triangular bipyramid (or dipyramid) is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.
As the name suggests, it can be constructed by joining two tetrahedra along one face. Although all its faces are congruent and the solid is face-transitive, it is not a Platonic solid because some vertices adjoin three faces and others adjoin four.
The bipyramid whose six faces are all equilateral triangles is one of the Johnson solids, (J12). A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966. As a Johnson solid with all faces equilateral triangles, it is also a deltahedron.
...
Wikipedia