Shrikhande graph

Shrikhande graph
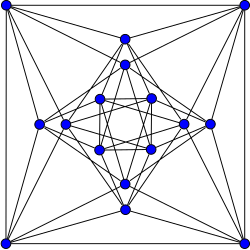
The Shrikhande graph
Named after	S. S. Shrikhande
Vertices	16
Edges	48
Radius	2
Diameter	2
Girth	3
Automorphisms	192
Chromatic number	4
Chromatic index	6
Properties	Strongly regular Hamiltonian Symmetric Eulerian Integral

In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having degree 6. Every pair of nodes has exactly two other neighbors in common, whether the pair of nodes is connected or not.

The Shrikhande graph can be constructed as a Cayley graph, where the vertex set is ${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{4}}$, and where two vertices are adjacent if and only if the difference is in ${\displaystyle \{\pm (1,0),\pm (0,1),\pm (1,1)\}}$.