Regular tetrahedron

Tetrahedral graph
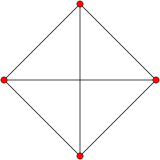Vertices	4
Edges	6
Radius	1
Diameter	1
Girth	3
Automorphisms	24
Chromatic number	4
Properties	Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph

In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons) is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces.

The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.

The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid".

Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.

For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces.

A regular tetrahedron is one in which all four faces are equilateral triangles. It is one of the five regular Platonic solids, which have been known since antiquity.

In a regular tetrahedron, not only are all its faces the same size and shape (congruent) but so are all its vertices and edges.

Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra they form the alternated cubic honeycomb, which is a tessellation.

...
Wikipedia