Regular dodecahedron
| Regular dodecahedron graph | |
|---|---|
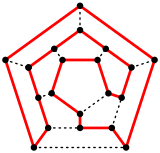
A Hamiltonian cycle in a dodecahedron.
|
|
| Vertices | 20 |
| Edges | 30 |
| Radius | 5 |
| Diameter | 5 |
| Girth | 5 |
| Automorphisms | 120 (S5) |
| Chromatic number | 3 |
| Properties | Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph |
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular composed of twelve regular pentagonal faces, with three meeting at each vertex, and is represented by the Schläfli symbol {5,3}. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals).
If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is
and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is
while the midradius, which touches the middle of each edge, is
These quantities may also be expressed as
where ϕ is the golden ratio.
Note that, given a regular dodecahedron of edge length one, ru is the radius of a circumscribing sphere about a cube of edge length ϕ, and ri is the apothem of a regular pentagon of edge length ϕ.
The surface area A and the volume V of a regular dodecahedron of edge length a are:
The regular dodecahedron has two special orthogonal projections, centered, on vertices and pentagonal faces, correspond to the A2 and H2Coxeter planes.
In perspective projection, viewed above a pentagonal face, the regular dodecahedron can be seen as a linear-edged schlegel diagram, or stereographic projection as a spherical polyhedron. These projections are also used in showing the four-dimensional 120-cell, a regular 4-dimensional polytope, constructed from 120 dodecahedra, projecting it down to 3-dimensions.
...
Wikipedia
