Logistic distribution

Logistic

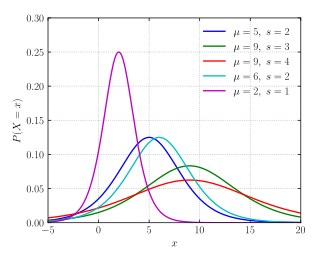
Probability density function
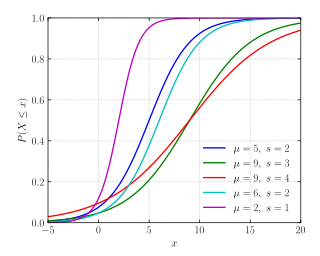
Cumulative distribution function
Parameters	μ location (real) s > 0 scale (real)
Support	x ∈ (−∞, ∞)
PDF	${\displaystyle {\frac {e^{-{\frac {x-\mu }{s}}}}{s\left(1+e^{-{\frac {x-\mu }{s}}}\right)^{2}}}\!}$
CDF	${\displaystyle {\frac {1}{1+e^{-{\frac {x-\mu }{s}}}}}\!}$
Mean	${\displaystyle \mu }$
Median	${\displaystyle \mu }$
Mode	${\displaystyle \mu }$
Variance	${\displaystyle {\tfrac {s^{2}\pi ^{2}}{3}}}$
Skewness	${\displaystyle 0}$
Ex. kurtosis	${\displaystyle 1.2}$
Entropy	${\displaystyle \ln(s)+2=\ln(\sigma )+1.404576,}$ where σ is the standard deviation.
MGF	${\displaystyle e^{\mu t}\operatorname {B} (1-st,1+st)}$ for st ∈ (−1, 1) Beta function
CF	${\displaystyle e^{it\mu }{\frac {\pi st}{\sinh(\pi st)}}}$

In probability theory and statistics, the logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears in logistic regression and feedforward neural networks. It resembles the normal distribution in shape but has heavier tails (higher kurtosis). The Tukey lambda distribution can be considered a generalization of the logistic distribution since it adds a shape parameter, λ, and corresponds to the logistic distribution when λ is zero.

The probability density function (pdf) of the logistic distribution is given by:

Because the pdf can be expressed in terms of the square of the hyperbolic secant function "sech", it is sometimes referred to as the sech-square(d) distribution.

The logistic distribution receives its name from its cumulative distribution function (cdf), which is an instance of the family of logistic functions. The cumulative distribution function of the logistic distribution is also a scaled version of the hyperbolic tangent.

In this equation, x is the random variable, μ is the mean, and s is a scale parameter proportional to the standard deviation.

The inverse cumulative distribution function (quantile function) of the logistic distribution is a generalization of the logit function. Its derivative is called the quantile density function. They are defined as follows: