Lévy distribution

Lévy (unshifted)

Probability density function
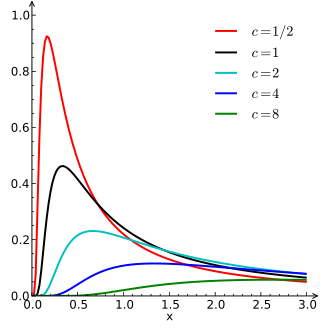Cumulative distribution function
Parameters	${\displaystyle \mu }$ location; ${\displaystyle c>0\,}$ scale
Support	${\displaystyle x\in [\mu ,\infty )}$
PDF	${\displaystyle {\sqrt {\frac {c}{2\pi }}}~~{\frac {e^{-{\frac {c}{2(x-\mu )}}}}{(x-\mu )^{3/2}}}}$
CDF	${\displaystyle {\textrm {erfc}}\left({\sqrt {\frac {c}{2(x-\mu )}}}\right)}$
Mean	${\displaystyle \infty }$
Median	${\displaystyle c/2({\textrm {erfc}}^{-1}(1/2))^{2}\,}$, for ${\displaystyle \mu =0}$
Mode	${\displaystyle {\frac {c}{3}}}$, for ${\displaystyle \mu =0}$
Variance	${\displaystyle \infty }$
Skewness	undefined
Ex. kurtosis	undefined
Entropy	${\displaystyle {\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}}$ where ${\displaystyle \gamma }$ is Euler's constant
MGF	undefined
CF	${\displaystyle e^{i\mu t-{\sqrt {-2ict}}}}$

${\displaystyle {\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}}$

In probability theory and statistics, the Lévy distribution, named after Paul Lévy, is a continuous probability distribution for a non-negative random variable. In spectroscopy, this distribution, with frequency as the dependent variable, is known as a van der Waals profile. It is a special case of the inverse-gamma distribution.

It is one of the few distributions that are stable and that have probability density functions that can be expressed analytically, the others being the normal distribution and the Cauchy distribution.

The probability density function of the Lévy distribution over the domain ${\displaystyle x\geq \mu }$ is