Herschel graph

Herschel graph
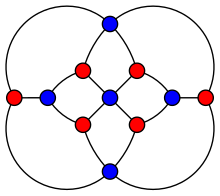
The Herschel graph.
Named after	Alexander Stewart Herschel
Vertices	11
Edges	18
Radius	3
Diameter	4
Girth	4
Automorphisms	12 (D6)
Chromatic number	2
Chromatic index	4
Properties	Polyhedral Planar Bipartite Perfect

In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges, the smallest non-Hamiltonian polyhedral graph. It is named after British astronomer Alexander Stewart Herschel, who wrote an early paper concerning William Rowan Hamilton's icosian game: the Herschel graph describes the smallest convex polyhedron for which this game has no solution. However, Herschel's paper described solutions for the Icosian game only on the graphs of the regular tetrahedron and regular icosahedron; it did not describe the Herschel graph.

The Herschel graph is a planar graph: it can be drawn in the plane with none of its edges crossing. It is also 3-vertex-connected: the removal of any two of its vertices leaves a connected subgraph. Therefore, by Steinitz's theorem, the Herschel graph is a polyhedral graph: there exists a convex polyhedron (an enneahedron) having the Herschel graph as its skeleton. The Herschel graph is also a bipartite graph: its vertices can be separated into two subsets of five and six vertices respectively, such that every edge has an endpoint in each subset (the red and blue subsets in the picture).

As with any bipartite graph, the Herschel graph is a perfect graph : the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph. It has also chromatic index 4, girth 4, radius 3 and diameter 4.