Grötzsch graph
| Grötzsch graph | |
|---|---|
 |
|
| Named after | Herbert Grötzsch |
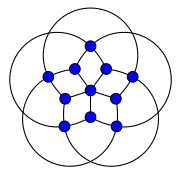
| Vertices | 11 |
| Edges | 20 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 10 (D5) |
| Chromatic number | 4 |
| Chromatic index | 5 |
| Properties |
Hamiltonian Triangle-free |
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch.
The Grötzsch graph is a member of an infinite sequence of triangle-free graphs, each the Mycielskian of the previous graph in the sequence, starting from the null graph; this sequence of graphs was used by Mycielski (1955) to show that there exist triangle-free graphs with arbitrarily large chromatic number. Therefore, the Grötzsch graph is sometimes also called the Mycielski graph or the Mycielski–Grötzsch graph. Unlike later graphs in this sequence, the Grötzsch graph is the smallest triangle-free graph with its chromatic number (Chvátal 1974).
The Grötzsch graph has chromatic index 5, radius 2, girth 4 and diameter 2. It is also a 3-vertex-connected and 3-edge-connected graph. The independence number is 5, and the domination number is 3.
The full automorphism group of the Grötzsch graph is isomorphic to the dihedral group D5 of order 10, the group of symmetries of a regular pentagon, including both rotations and reflections.
The characteristic polynomial of the Grötzsch graph is
The existence of the Grötzsch graph demonstrates that the assumption of planarity is necessary in Grötzsch's theorem (Grötzsch 1959) that every triangle-free planar graph is 3-colorable.
...
Wikipedia
