Generalized inverse Gaussian distribution

Generalized inverse Gaussian

Probability density function
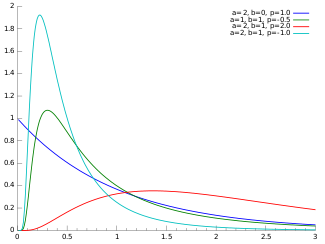
Parameters	a > 0, b > 0, p real
Support	x > 0
PDF	${\displaystyle f(x)={\frac {(a/b)^{p/2}}{2K_{p}({\sqrt {ab}})}}x^{(p-1)}e^{-(ax+b/x)/2}}$
Mean	${\displaystyle \operatorname {E} [x]={\frac {{\sqrt {b}}\ K_{p+1}({\sqrt {ab}})}{{\sqrt {a}}\ K_{p}({\sqrt {ab}})}}}$ ${\displaystyle \operatorname {E} [x^{-1}]={\frac {{\sqrt {a}}\ K_{p+1}({\sqrt {ab}})}{{\sqrt {b}}\ K_{p}({\sqrt {ab}})}}-{\frac {2p}{b}}}$ ${\displaystyle \operatorname {E} [\ln x]=\ln {\frac {\sqrt {b}}{\sqrt {a}}}+{\frac {\partial }{\partial p}}\ln K_{p}({\sqrt {ab}})}$
Mode	${\displaystyle {\frac {(p-1)+{\sqrt {(p-1)^{2}+ab}}}{a}}}$
Variance	${\displaystyle \left({\frac {b}{a}}\right)\left[{\frac {K_{p+2}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}-\left({\frac {K_{p+1}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}\right)^{2}\right]}$
MGF	${\displaystyle \left({\frac {a}{a-2t}}\right)^{\frac {p}{2}}{\frac {K_{p}({\sqrt {b(a-2t)}})}{K_{p}({\sqrt {ab}})}}}$
CF	${\displaystyle \left({\frac {a}{a-2it}}\right)^{\frac {p}{2}}{\frac {K_{p}({\sqrt {b(a-2it)}})}{K_{p}({\sqrt {ab}})}}}$

In probability theory and statistics, the generalized inverse Gaussian distribution (GIG) is a three-parameter family of continuous probability distributions with probability density function

where K_p is a modified Bessel function of the second kind, a > 0, b > 0 and p a real parameter. It is used extensively in geostatistics, statistical linguistics, finance, etc. This distribution was first proposed by Étienne Halphen. It was rediscovered and popularised by Ole Barndorff-Nielsen, who called it the generalized inverse Gaussian distribution. It is also known as the Sichel distribution, after Herbert Sichel. Its statistical properties are discussed in Bent Jørgensen's lecture notes.

Barndorff-Nielsen and Halgreen proved that the GIG distribution is infinitely divisible.

The entropy of the generalized inverse Gaussian distribution is given as

where ${\displaystyle \left[{\frac {d}{d\nu }}K_{\nu }\left({\sqrt {ab}}\right)\right]_{\nu =p}}$ is a derivative of the modified Bessel function of the second kind with respect to the order ${\displaystyle \nu }$ evaluated at ${\displaystyle \nu =p}$