Equilateral

Equilateral triangle
Type	Regular polygon
Edges and vertices	3
Schläfli symbol	{3}
Coxeter diagram
Symmetry group	D3
Area	${\displaystyle {\tfrac {\sqrt {3}}{4}}a^{2}}$
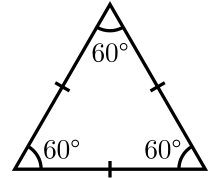
Internal angle (degrees)	60°

In geometry, an equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, equilateral triangles are also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. They are regular polygons, and can therefore also be referred to as regular triangles.

Denoting the common length of the sides of the equilateral triangle as a, we can determine using the Pythagorean theorem that:

Denoting the radius of the circumscribed circle as R, we can determine using trigonometry that:

Many of these quantities have simple relationships to the altitude ("h") of each vertex from the opposite side:

In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors and the medians to each side coincide.

A triangle ABC that has the sides a, b, c, semiperimeter s, area T, exradii r_a, r_b, r_c (tangent to a, b, c respectively), and where R and r are the radii of the circumcircle and incircle respectively, is equilateral if and only if any one of the statements in the following nine categories is true. Thus these are properties that are unique to equilateral triangles.

Three kinds of cevians are equal for (and only for) equilateral triangles:

Every triangle center of an equilateral triangle coincides with its centroid, which implies that the equilateral triangle is the only triangle with no Euler line connecting some of the centers. For some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral. In particular:

...
Wikipedia