Coxeter graph
| Coxeter graph | |
|---|---|
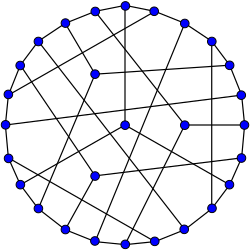
The Coxeter graph
|
|
| Named after | H. S. M. Coxeter |
| Vertices | 28 |
| Edges | 42 |
| Radius | 4 |
| Diameter | 4 |
| Girth | 7 |
| Automorphisms | 336 (PGL2(7)) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties |
Symmetric Distance-regular Distance-transitive Cubic Hypohamiltonian |
In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. All the cubic distance-regular graphs are known. The Coxeter graph is one of the 13 such graphs. It is named after Harold Scott MacDonald Coxeter.
The Coxeter graph has chromatic number 3, chromatic index 3, radius 4, diameter 4 and girth 7. It is also a 3-vertex-connected graph and a 3-edge-connected graph.
The Coxeter graph is hypohamiltonian: it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It has rectilinear crossing number 11, and is the smallest cubic graph with that crossing number currently known, but an 11-crossing, 26-vertex graph may exist (sequence in the OEIS).
The simplest construction of a Coxeter graph is from a Fano plane. Take the 7C3 = 35 possible 3-combinations on 7 objects. Discard the 7 triplets that correspond to the lines of the Fano plane, leaving 28 triplets. Link two triplets if they are disjoint. The result is the Coxeter graph.
The Coxeter graph may also be constructed from the smaller distance-regular Heawood graph by constructing a vertex for each 6-cycle in the Heawood graph and an edge for each disjoint pair of 6-cycles.
The Coxeter graph may be derived from the Hoffman-Singleton graph. Take any vertex v in the Hoffman-Singleton graph. There is an independent set of size 15 that includes v. Delete the 7 neighbors of v, and the whole independent set including v, leaving behind the Coxeter graph.
...
Wikipedia
