Continuous uniform distribution

Uniform

Probability density function 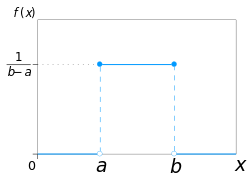Using maximum convention
Cumulative distribution function
Notation	${\displaystyle {\mathcal {U}}(a,b)}$ or ${\displaystyle \mathrm {unif} (a,b)}$
Parameters	${\displaystyle -\infty <a<b<\infty \,}$
Support	${\displaystyle x\in [a,b]}$
PDF	${\displaystyle {\begin{cases}{\frac {1}{b-a}}&{\text{for }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}}$
CDF	${\displaystyle {\begin{cases}0&{\text{for }}x<a\\{\frac {x-a}{b-a}}&{\text{for }}x\in [a,b)\\1&{\text{for }}x\geq b\end{cases}}}$
Mean	${\displaystyle {\tfrac {1}{2}}(a+b)}$
Median	${\displaystyle {\tfrac {1}{2}}(a+b)}$
Mode	any value in ${\displaystyle (a,b)}$
Variance	${\displaystyle {\tfrac {1}{12}}(b-a)^{2}}$
Skewness	0
Ex. kurtosis	${\displaystyle -{\tfrac {6}{5}}}$
Entropy	${\displaystyle \log(b-a)\,}$
MGF	${\displaystyle {\begin{cases}{\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(b-a)}}&{\text{for }}t\neq 0\\1&{\text{for }}t=0\end{cases}}}$
CF	${\displaystyle {\frac {\mathrm {e} ^{itb}-\mathrm {e} ^{ita}}{it(b-a)}}}$

In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by the two parameters, a and b, which are its minimum and maximum values. The distribution is often abbreviated U(a,b). It is the maximum entropy probability distribution for a random variate X under no constraint other than that it is contained in the distribution's support.

The probability density function of the continuous uniform distribution is:

The values of f(x) at the two boundaries a and b are usually unimportant because they do not alter the values of the integrals of f(x) dx over any interval, nor of x f(x) dx or any higher moment. Sometimes they are chosen to be zero, and sometimes chosen to be 1/(b − a). The latter is appropriate in the context of estimation by the method of maximum likelihood. In the context of Fourier analysis, one may take the value of f(a) or f(b) to be 1/(2(b − a)), since then the inverse transform of many integral transforms of this uniform function will yield back the function itself, rather than a function which is equal "almost everywhere", i.e. except on a set of points with zero measure. Also, it is consistent with the sign function which has no such ambiguity.

In terms of mean μ and variance σ², the probability density may be written as:

The cumulative distribution function is: