Beta distribution

Beta

Probability density function
Cumulative distribution function
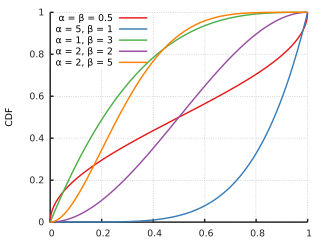
Notation	Beta(α, β)
Parameters	α > 0 shape (real) β > 0 shape (real)
Support	${\displaystyle x\in [0,1]\!}$ or ${\displaystyle x\in (0,1)\!}$
PDF	${\displaystyle {\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\!}$ where ${\displaystyle \mathrm {B} (\alpha ,\beta )={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}}$
CDF	${\displaystyle I_{x}(\alpha ,\beta )\!}$ (the incomplete beta function)
Mean	${\displaystyle \operatorname {E} [X]={\frac {\alpha }{\alpha +\beta }}\!}$ ${\displaystyle \operatorname {E} [\ln X]=\psi (\alpha )-\psi (\alpha +\beta )\!}$ (see digamma function and see section: Geometric mean)
Median	${\displaystyle {\begin{matrix}I_{\frac {1}{2}}^{[-1]}(\alpha ,\beta ){\text{ (in general) }}\\[0.5em]\approx {\frac {\alpha -{\tfrac {1}{3}}}{\alpha +\beta -{\tfrac {2}{3}}}}{\text{ for }}\alpha ,\beta >1\end{matrix}}}$
Mode	${\displaystyle {\frac {\alpha -1}{\alpha +\beta -2}}\!}$ for α, β >1
Variance	${\displaystyle \operatorname {var} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}\!}$ ${\displaystyle \operatorname {var} [\ln X]=\psi _{1}(\alpha )-\psi _{1}(\alpha +\beta )\!}$ (see trigamma function and see section: Geometric variance)
Skewness	${\displaystyle {\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}}$
Ex. kurtosis	${\displaystyle {\frac {6[(\alpha -\beta )^{2}(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)]}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}}$
Entropy	${\displaystyle {\begin{matrix}\ln \mathrm {B} (\alpha ,\beta )-(\alpha -1)\psi (\alpha )-(\beta -1)\psi (\beta )\\[0.5em]+(\alpha +\beta -2)\psi (\alpha +\beta )\end{matrix}}}$
MGF	${\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}}$
CF	${\displaystyle {}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)\!}$ (see Confluent hypergeometric function)
Fisher information	${\displaystyle {\begin{matrix}\\\operatorname {var} [\ln X]&\operatorname {cov} [\ln X,\ln(1-X)]\\\operatorname {cov} [\ln X,\ln(1-X)]&\operatorname {var} [\ln(1-X)]\end{matrix}}}$ see section: Fisher information matrix

${\displaystyle I_{x}(\alpha ,\beta )\!}$

In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] parametrized by two positive shape parameters, denoted by α and β, that appear as exponents of the random variable and control the shape of the distribution.

The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. For example, it has been used as a statistical description of allele frequencies in population genetics; time allocation in project management / control systems; sunshine data; variability of soil properties; proportions of the minerals in rocks in stratigraphy; and heterogeneity in the probability of HIV transmission.

In Bayesian inference, the beta distribution is the conjugate prior probability distribution for the Bernoulli, binomial, negative binomial and geometric distributions. For example, the beta distribution can be used in Bayesian analysis to describe initial knowledge concerning probability of success such as the probability that a space vehicle will successfully complete a specified mission. The beta distribution is a suitable model for the random behavior of percentages and proportions.