Yule distribution

Yule–Simon

Probability mass function Yule–Simon PMF on a log-log scale. (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.)
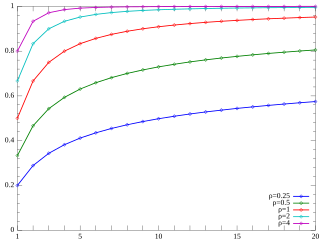
Cumulative distribution function Yule–Simon CMF. (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.)
Parameters	${\displaystyle \rho >0\,}$ shape (real)
Support	${\displaystyle k\in \{1,2,\dotsc \}}$
pmf	${\displaystyle \rho \operatorname {B} (k,\rho +1)}$
CDF	${\displaystyle 1-k\operatorname {B} (k,\rho +1)}$
Mean	${\displaystyle {\frac {\rho }{\rho -1}}}$ for ${\displaystyle \rho >1}$
Mode	${\displaystyle 1}$
Variance	${\displaystyle {\frac {\rho ^{2}}{(\rho -1)^{2}(\rho -2)}}}$ for ${\displaystyle \rho >2}$
Skewness	${\displaystyle {\frac {(\rho +1)^{2}{\sqrt {\rho -2}}}{(\rho -3)\rho }}\,}$ for ${\displaystyle \rho >3}$
Ex. kurtosis	${\displaystyle \rho +3+{\frac {11\rho ^{3}-49\rho -22}{(\rho -4)(\rho -3)\rho }}}$ for ${\displaystyle \rho >4}$
MGF	${\displaystyle {\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{t})\,e^{t}}$
CF	${\displaystyle {\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{i\,t})e^{i\,t}}$

In probability and statistics, the Yule–Simon distribution is a discrete probability distribution named after Udny Yule and Herbert A. Simon. Simon originally called it the Yule distribution.

The probability mass function (pmf) of the Yule–Simon (ρ) distribution is

for integer ${\displaystyle k\geq 1}$ and real ${\displaystyle \rho >0}$, where ${\displaystyle \operatorname {B} }$ is the beta function. Equivalently the pmf can be written in terms of the falling factorial as