Uniform distribution (discrete)

discrete uniform

Probability mass function n = 5 where n = b − a + 1
Cumulative distribution function
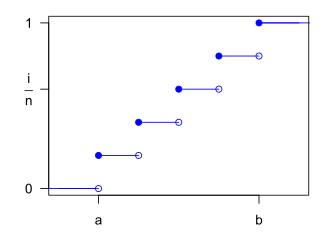Notation	${\displaystyle {\mathcal {U}}\{a,b\}}$ or ${\displaystyle \mathrm {unif} \{a,b\}}$
Parameters	${\displaystyle a\in \{\dots ,-2,-1,0,1,2,\dots \}\,}$ ${\displaystyle b\in \{\dots ,-2,-1,0,1,2,\dots \},b\geq a}$ ${\displaystyle n=b-a+1\,}$
Support	${\displaystyle k\in \{a,a+1,\dots ,b-1,b\}\,}$
pmf	${\displaystyle {\frac {1}{n}}}$
CDF	${\displaystyle {\frac {\lfloor k\rfloor -a+1}{n}}}$
Mean	${\displaystyle {\frac {a+b}{2}}\,}$
Median	${\displaystyle {\frac {a+b}{2}}\,}$
Mode	N/A
Variance	${\displaystyle {\frac {(b-a+1)^{2}-1}{12}}}$
Skewness	${\displaystyle 0\,}$
Ex. kurtosis	${\displaystyle -{\frac {6(n^{2}+1)}{5(n^{2}-1)}}\,}$
Entropy	${\displaystyle \ln(n)\,}$
MGF	${\displaystyle {\frac {e^{at}-e^{(b+1)t}}{n(1-e^{t})}}\,}$
CF	${\displaystyle {\frac {e^{iat}-e^{i(b+1)t}}{n(1-e^{it})}}}$

In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution whereby a finite number of values are equally likely to be observed; every one of n values has equal probability 1/n. Another way of saying discrete uniform distribution would be a known, finite number of outcomes equally likely to happen.

A simple example of the discrete uniform distribution is throwing a fair die. The possible values are 1, 2, 3, 4, 5, 6, and each time the die is thrown the probability of a given score is 1/6. If two dice are thrown and their values added, the resulting distribution is no longer uniform since not all sums have equal probability.

The discrete uniform distribution itself is inherently non-parametric. It is convenient, however, to represent its values generally by an integer interval [a,b], so that a,b become the main parameters of the distribution (often one simply considers the interval [1,n] with the single parameter n). With these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any k ∈ [a,b], as

This example is described by saying that a sample of k observations is obtained from a uniform distribution on the integers ${\displaystyle 1,2,\dotsc ,N}$, with the problem being to estimate the unknown maximum N. This problem is commonly known as the German tank problem, following the application of maximum estimation to estimates of German tank production during World War II.