Truncated icosidodecahedral graph

Truncated icosidodecahedral graph
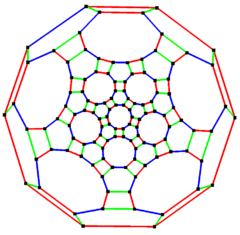
5-fold symmetry
Vertices	120
Edges	180
Radius	15
Diameter	15
Girth	4
Automorphisms	120 (A5×2)
Chromatic number	2
Properties	Cubic, Hamiltonian, regular, zero-symmetric

In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

It has 62 faces: 30 squares, 20 regular hexagons, and 12 regular decagons. It has more vertices (120) and edges (180) than any other convex nonprismatic uniform polyhedron. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated icosidodecahedron is a zonohedron.

Alternate interchangeable names include:

The name truncated icosidodecahedron, originally given by Johannes Kepler, is somewhat misleading. If one truncates an icosidodecahedron by cutting the corners off, one does not get this uniform figure: instead of squares the truncation has golden rectangles. However, the resulting figure is topologically equivalent to this and can always be deformed until the faces are regular.

The alternative name great rhombicosidodecahedron (as well as rhombitruncated icosidodecahedron) refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron, which is dual to the icosidodecahedron. Compare to small rhombicosidodecahedron.

One unfortunate point of confusion is that there is a nonconvex uniform polyhedron of the same name. See nonconvex great rhombicosidodecahedron.

...
Wikipedia