Third stellation of icosahedron

In geometry, the excavated dodecahedron is a star polyhedron having 60 equilateral triangular faces. Its exterior surface represents the Ef₁g₁ stellation of the icosahedron. It appears in Magnus Wenninger's book Polyhedron Models as model 28, the third stellation of icosahedron.

It has the same external form as a certain facetting of the dodecahedron having 20 self-intersecting hexagons as faces. The non-convex hexagon face can be broken up into four equilateral triangles, three of which are the same size. A true excavated dodecahedron has the three congruent equilateral triangles as true faces of the polyhedron, while the interior equilateral triangle is not present.

The 20 vertices of the convex hull match the vertex arrangement of the dodecahedron.

One of the star hexagon faces highlighted.

Its face as a facet of the dodecahedron.

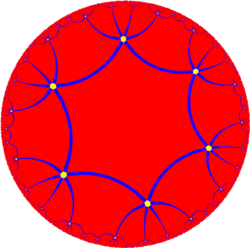
The faceting is a noble polyhedron. With six six-sided faces around each vertex, it is topologically equivalent to a quotient space of the hyperbolic order-6 hexagonal tiling, {6,6} and is an abstract type {6,6}₆. It is one of 10 abstract regular polyhedron of index two with vertices on one orbit.

...
Wikipedia