Star polyhedra

In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.

There are two general kinds of star polyhedron:

Mathematical studies of star polyhedra are usually concerned with regular, uniform polyhedra, or the duals of the uniform polyhedra. All these stars are of the self-intersecting kind.

The regular star polyhedra are self-intersecting polyhedra. They may either have self-intersecting faces, or self-intersecting vertex figures.

There are four regular star polyhedra, known as the Kepler-Poinsot polyhedra. The Schläfli symbol {p,q} implies faces with p sides, and vertex figures with q sides. Two of them have pentagrammic {5/2} faces and two have pentagrammic vertex figures.

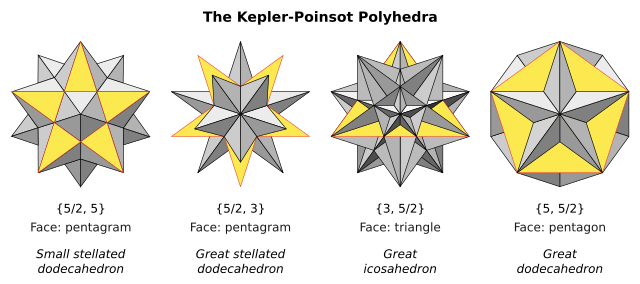
These images show each form with a single face colored yellow to show the visible portion of that face.

There are many uniform star polyhedra including two infinite series, of prisms and of antiprisms, and their duals.

The uniform and dual uniform star polyhedra are also self-intersecting polyhedra. They may either have self-intersecting faces, or self-intersecting vertex figures or both.

...
Wikipedia