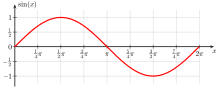
Sine function
| Sine | |
|---|---|
 |
|
| Basic features | |
| Parity | odd |
| Domain | (−∞,∞) a |
| Codomain | [−1,1] a |
| Period | 2π |
|
|
|
| Specific values | |
| At zero | 0 |
| Maxima | ((2k + ½)π, 1) b |
| Minima | ((2k − ½)π, −1) |
|
|
|
| Specific features | |
| Root | kπ |
| Critical point | kπ − π/2 |
| Inflection point | kπ |
| Fixed point | 0 |
|
|
|
|
|
|
In mathematics, the sine is a trigonometric function of an angle. The sine of an acute angle is defined in the context of a right triangle: for the specified angle, it is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse).
More generally, the definition of sine (and other trigonometric functions) can be extended to any real value in terms of the length of a certain line segment in a unit circle. More modern definitions express the sine as an infinite series or as the solution of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers.
The sine function is commonly used to model periodic phenomena such as sound and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year.
The function sine can be traced to the jyā and koṭi-jyā functions used in Gupta period Indian astronomy (Aryabhatiya, Surya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin. The word "sine" comes from a Latin mistranslation of the Arabic jiba, which is a transliteration of the Sanskrit word for half the chord, jya-ardha.
To define the trigonometric functions for an acute angle α, start with any right triangle that contains an angle of measure α; in the accompanying figure, angle A in triangle ABC has measure α. The three sides of the triangle are named as follows:
...
Wikipedia
