Regular hexagon

Regular hexagon
A regular hexagon
Type	Regular polygon
Edges and vertices	6
Schläfli symbol	{6}, t{3}
Coxeter diagram
Symmetry group	Dihedral (D6), order 2×6
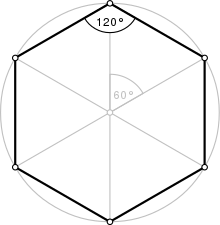
Internal angle (degrees)	120°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a hexagon (from Greek ἕξ hex, "six" and γωνία, gonía, "corner, angle") is a six sided polygon or 6-gon. The total of the internal angles of any hexagon is 720°.

A regular hexagon has Schläfli symbol {6} and can also be constructed as a truncated equilateral triangle, t{3}, which alternates two types of edges.

A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle).

The common length of the sides equals the radius of the circumscribed circle, which equals ${\displaystyle {\tfrac {2{\sqrt {3}}}{3}}}$ times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has 6 rotational symmetries (rotational symmetry of order six) and 6 reflection symmetries (six lines of symmetry), making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.