Potential flow








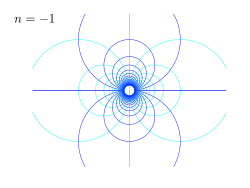
Examples of conformal maps for the power law $w = Az n$ , for different values of the power $n$ . Shown is the $z$ -plane, showing lines of constant potential $φ$ and streamfunction $ψ$ , while $w = φ + iψ$ .

In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero.

In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows. The potential flow approach occurs in the modeling of both stationary as well as nonstationary flows.

Applications of potential flow are for instance: the outer flow field for aerofoils, water waves, electroosmotic flow, and groundwater flow. For flows (or parts thereof) with strong vorticity effects, the potential flow approximation is not applicable.

In fluid dynamics, a potential flow is described by means of a velocity potential $φ$ , being a function of space and time. The flow velocity $v$ is a vector field equal to the gradient, $\nabla$ , of the velocity potential $φ$ :

Sometimes, also the definition $v = -\nabla φ$ , with a minus sign, is used. But here we will use the definition above, without the minus sign. From vector calculus it is known, that the curl of a gradient is equal to zero:

...
Wikipedia