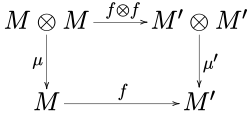Monoid object

In category theory, a monoid (or monoid object) (M, μ, η) in a monoidal category (C, ⊗, I) is an object M together with two morphisms

such that the pentagon diagram

and the unitor diagram

commute. In the above notations, I is the unit element and α, λ and ρ are respectively the associativity, the left identity and the right identity of the monoidal category C.

Dually, a comonoid in a monoidal category C is a monoid in the dual category C^op.

Suppose that the monoidal category C has a symmetry γ. A monoid M in C is commutative when μ o γ = μ.

Given two monoids (M, μ, η) and (M ', μ', η') in a monoidal category C, a morphism f : M → M ' is a morphism of monoids when

In other words, the following diagrams

,

commute.

The category of monoids in C and their monoid morphisms is written Mon_C.

...
Wikipedia