Hosohedron

Set of regular n-gonal hosohedra
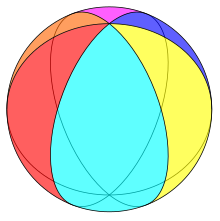
Example hexagonal hosohedron on a sphere
Type	Regular polyhedron or spherical tiling
Faces	n digons
Edges	n
Vertices	2
χ	2
Vertex configuration	2n
Wythoff symbol	n | 2 2
Schläfli symbol	{2,n}
Coxeter diagram
Symmetry group	Dnh, [2,n], (*22n), order 4n
Rotation group	Dn, [2,n]+, (22n), order 2n
Dual polyhedron	dihedron

In geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.

A regular n-gonal hosohedron has Schläfli symbol {2, n}, with each spherical lune having internal angle 2π/n radians (360/n degrees).

For a regular polyhedron whose Schläfli symbol is {m, n}, the number of polygonal faces may be found by:

The Platonic solids known to antiquity are the only integer solutions for m ≥ 3 and n ≥ 3. The restriction m ≥ 3 enforces that the polygonal faces must have at least three sides.

When considering polyhedra as a spherical tiling, this restriction may be relaxed, since digons (2-gons) can be represented as spherical lunes, having non-zero area. Allowing m = 2 admits a new infinite class of regular polyhedra, which are the hosohedra. On a spherical surface, the polyhedron {2, n} is represented as n abutting lunes, with interior angles of 2π/n. All these lunes share two common vertices.