Heptadecagon

Regular heptadecagon
A regular heptadecagon
Type	Regular polygon
Edges and vertices	17
Schläfli symbol	{17}
Coxeter diagram
Symmetry group	Dihedral (D17), order 2×17
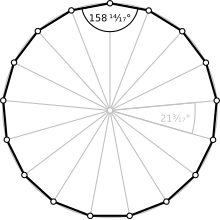
Internal angle (degrees)	≈158.82°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a heptadecagon or 17-gon is a seventeen-sided polygon.

A regular heptadecagon is represented by the Schläfli symbol {17}.

As 17 is a Fermat prime, the regular heptadecagon is a constructible polygon (that is, one that can be constructed using a compass and unmarked straightedge): this was shown by Carl Friedrich Gauss in 1796 at the age of 19. This proof represented the first progress in regular polygon construction in over 2000 years. Gauss's proof relies firstly on the fact that constructibility is equivalent to expressibility of the trigonometric functions of the common angle in terms of arithmetic operations and square root extractions, and secondly on his proof that this can be done if the odd prime factors of n are distinct Fermat primes, which are of the form ${\displaystyle \scriptstyle F_{n}=2^{2^{\overset {n}{}}}+1}$. Constructing a regular heptadecagon thus involves finding the cosine of ${\displaystyle 2\pi /17}$ in terms of square roots, which involves an equation of degree 17—a Fermat prime. Gauss' book Disquisitiones Arithmeticae gives this as (in modern notation):