Gyroelongated square bipyramid
| Gyroelongated square bipyramid | |
|---|---|
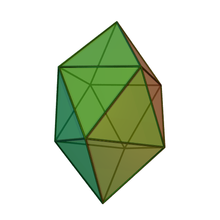 |
|
| Type |
Johnson J16 - J17 - J18 |
| Faces | 2.8 triangles |
| Edges | 24 |
| Vertices | 10 |
| Vertex configuration | 2(34) 8(35) |
| Symmetry group | D4d, [2+,8], (2*4) |
| Rotation group | D4, [2,4]+, (422) |
| Dual polyhedron | Truncated square trapezohedron |
| Properties | convex, deltahedron |
| Net | |
 |
|
In geometry, the gyroelongated square bipyramid or heccaidecadeltahedron is one of the Johnson solids (J17). As the name suggests, it can be constructed by gyroelongating an octahedron (square bipyramid) by inserting a square antiprism between its congruent halves. It is a deltahedron.
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
The dual of the gyroelongated square bipyramid is a square truncated trapezohedron with 10 faces: 8 pentagons and 2 square.
...
Wikipedia
