Gray graph

Gray graph
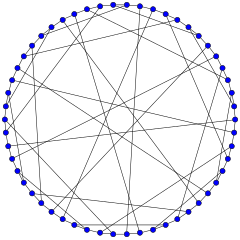
The Gray graph
Named after	Marion Cameron Gray
Vertices	54
Edges	81
Radius	6
Diameter	6
Girth	8
Automorphisms	1296
Chromatic number	2
Chromatic index	3
Properties	Cubic Semi-symmetric Hamiltonian Bipartite

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive (see below).

The Gray graph has chromatic number 2, chromatic index 3, radius 6 and diameter 6. It is also a 3-vertex-connected and 3-edge-connected non-planar graph.

The Gray graph can be constructed (Bouwer 1972) from the 27 points of a 3×3×3 grid and the 27 axis-parallel lines through these points. This collection of points and lines forms a projective configuration: each point has exactly three lines through it, and each line has exactly three points on it. The Gray graph is the Levi graph of this configuration; it has a vertex for every point and every line of the configuration, and an edge for every pair of a point and a line that touch each other. This construction generalizes (Bouwer 1972) to any dimension n ≥ 3, yielding an n-valent Levi graph with algebraic properties similar to those of the Gray graph. In (Monson, Pisanski, Schulte, Ivic-Weiss 2007), the Gray graph appears as a different sort of Levi graph for the edges and triangular faces of a certain locally toroidal abstract regular 4-polytope. It is therefore the first in an infinite family of similarly constructed cubic graphs.

...
Wikipedia