Friendship graph
| Friendship graph | |
|---|---|
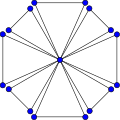
The friendship graph F8.
|
|
| Vertices | 2n+1 |
| Edges | 3n |
| Radius | 1 |
| Diameter | 2 |
| Girth | 3 |
| Chromatic number | 3 |
| Chromatic index | 2n |
| Properties |
Unit distance Planar Eulerian factor-critical |
| Notation | Fn |
In the mathematical field of graph theory, the friendship graph (or Dutch windmill graph or n-fan) Fn is a planar undirected graph with 2n+1 vertices and 3n edges.
The friendship graph Fn can be constructed by joining n copies of the cycle graph C3 with a common vertex.
By construction, the friendship graph Fn is isomorphic to the windmill graph Wd(3,n). It is unit distance with girth 3, diameter 2 and radius 1. The graph F2 is isomorphic to the butterfly graph.
The friendship theorem of Paul Erdős, Alfréd Rényi, and Vera T. Sós (1966) states that the finite graphs with the property that every two vertices have exactly one neighbor in common are exactly the friendship graphs. Informally, if a group of people has the property that every pair of people has exactly one friend in common, then there must be one person who is a friend to all the others. However, for infinite graphs, there can be many different graphs with the same cardinality that have this property.
A combinatorial proof of the friendship theorem was given by Mertzios and Unger. Another proof was given by Craig Huneke.
The friendship graph has chromatic number 3 and chromatic index 2n. Its chromatic polynomial can be deduced from the chromatic polynomial of the cycle graph C3 and is equal to .
...
Wikipedia

