Elongated square gyrobicupola
| Elongated square gyrobicupola | |
|---|---|
 |
|
| Type |
Johnson J36 - J37 - J38 |
| Faces | 8 triangles 18 squares |
| Edges | 48 |
| Vertices | 24 |
| Vertex configuration | 8+16(3.43) |
| Symmetry group | D4d |
| Dual polyhedron | Pseudo-deltoidal icositetrahedron |
| Properties | convex, singular vertex figure |
| Net | |
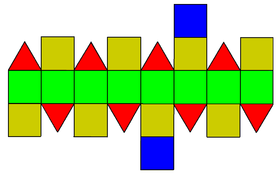 |
|
In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids (J37). It is not usually considered to be an Archimedean solid, even though its faces consist of regular polygons that meet in the same pattern at each of its vertices, because unlike the 13 Archimedean solids, it lacks a set of global symmetries that take every vertex to every other vertex (though Grünbaum has suggested it should be added to the traditional list of Archimedean solids as a 14th example).
This shape may have been discovered by Johannes Kepler in his enumeration of the Archimedean solids, but its first clear appearance in print appears to be the work of Duncan Sommerville in 1905. It was independently rediscovered by J. C. P. Miller by 1930 (by mistake while attempting to construct a model of the rhombicuboctahedron ) and again by V. G. Ashkinuse in 1957.
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
As the name suggests, it can be constructed by elongating a square gyrobicupola (J29) and inserting an octagonal prism between its two halves.
...
Wikipedia
