Dodecagon
| Regular dodecagon | |
|---|---|
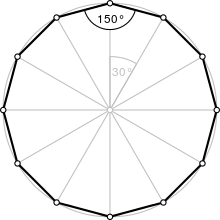
A regular dodecagon
|
|
| Type | Regular polygon |
| Edges and vertices | 12 |
| Schläfli symbol | {12}, t{6}, tt{3} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D12), order 2×12 |
| Internal angle (degrees) | 150° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a dodecagon or 12-gon is any twelve-sided polygon.
A regular dodecagon is a closed figure with sides of the same length and internal angles of the same size. It has twelve lines of reflective symmetry and rotational symmetry of order 12. A regular dodecagon is represented by the Schläfli symbol {12} and can be constructed as a truncated hexagon, t{6}, or a twice-truncated triangle, tt{3}. The internal angle at each vertex of a regular dodecagon is 150°.
The area of a regular dodecagon of side length a is given by:
And in terms of the apothem r (see also inscribed figure), the area is:
In terms of the circumradius R, the area is:
The span of the dodecagon is the distance between two parallel sides and is equal to twice the apothem. A simple formula for area (given side length and span) is:
This can be verified with the trigonometric relationship:
The perimeter of a regular dodecagon in terms of apothem is:
The perimeter in terms of circumradius is:
This coefficient is double the coefficient found in the apothem equation for area.
As 12 = 22 × 3, regular dodecagon is constructible using compass and straightedge:
Coxeter states that every parallel-sided 2m-gon can be divided into m(m-1)/2 rhombs. For the dodecagon, m=6, and it can be divided into 15 rhombs, with one example shown below. This decomposition is based on a Petrie polygon projection of a 6-cube, with 15 of 240 faces.
One of the ways the mathematical manipulative pattern blocks are used is in creating a number of different dodecagons.
...
Wikipedia
