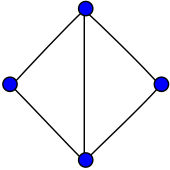
Diamond graph
| Diamond graph | |
|---|---|
 |
|
| Vertices | 4 |
| Edges | 5 |
| Radius | 1 |
| Diameter | 2 |
| Girth | 3 |
| Automorphisms | 4 (Z/2Z×Z/2Z) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties |
Hamiltonian Planar Unit distance |
In the mathematical field of graph theory, the diamond graph is a planar undirected graph with 4 vertices and 5 edges. It consists of a complete graph minus one edge.
The diamond graph has radius 1, diameter 2, girth 3, chromatic number 3 and chromatic index 3. It is also a 2-vertex-connected and a 2-edge-connected gracefulHamiltonian graph.
A graph is diamond-free if it has no diamond as an induced subgraph. The triangle-free graphs are diamond-free graphs, since every diamond contains a triangle. The diamond-free graphs are locally clustered: that is, they are the graphs in which every neighborhood is a cluster graph.
The family of graphs in which each connected component is a cactus graph is downwardly closed under graph minor operations. This graph family may be characterized by a single forbidden minor. This minor is the diamond graph.
...
Wikipedia

