Copeland's method

Copeland's method or Copeland's pairwise aggregation method is a Condorcet method in which candidates are ordered by the number of pairwise victories, minus the number of pairwise defeats. It was invented by Ramon Llull in his 1299 treatise Ars Electionis, but his form only counted pairwise victories and not defeats (which could lead to a different result in the case of a pairwise tie).

Proponents argue that this method is easily understood by the general populace, which is generally familiar with the sporting equivalent. In many round-robin tournaments, the winner is the competitor with the most victories. It is also easy to calculate.

When there is no Condorcet winner (i.e., when there are multiple members of the Smith set), this method often leads to ties. For example, if there is a three-candidate majority rule cycle, each candidate will have exactly one loss, and there will be an unresolved tie between the three.

Critics argue that it also puts too much emphasis on the quantity of pairwise victories and defeats rather than their magnitudes.

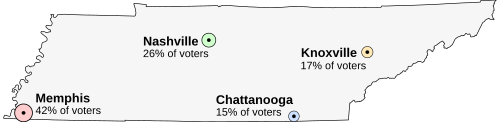
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

The preferences of the voters would be divided like this:

...
Wikipedia