Coombs' method

Coombs' method (or the Coombs rule) is a ranked voting system created by Clyde Coombs used for single-winner elections. Similarly to instant-runoff voting, it uses candidate elimination and redistribution of votes cast for that candidate until one candidate has a majority of votes.

Each voter rank-orders all of the candidates on their ballot. If at any time one candidate is ranked first (among non-eliminated candidates) by an absolute majority of the voters, that candidate wins. Otherwise, the candidate ranked last (again among non-eliminated candidates) by the largest number of (or a plurality of) voters is eliminated. Conversely, under instant-runoff voting, the candidate ranked first (among non-eliminated candidates) by the fewest voters is eliminated.

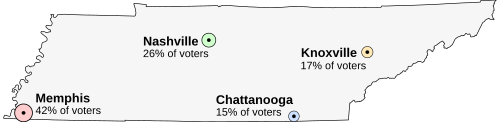
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

The preferences of the voters would be divided like this:

Assuming all of the voters vote sincerely (strategic voting is discussed below), the results would be as follows, by percentage:

...
Wikipedia