Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.
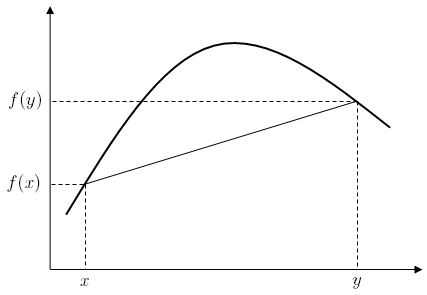
A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be concave if, for any x and y in the interval and for any α in [0,1],
A function is called strictly concave if
for any α in (0,1) and x ≠ y.
For a function f:R→R, this definition merely states that for every z between x and y, the point (z, f(z) ) on the graph of f is above the straight line joining the points (x, f(x) ) and (y, f(y) ).
A function f is quasiconcave if the upper contour sets of the function are convex sets.
...
Wikipedia