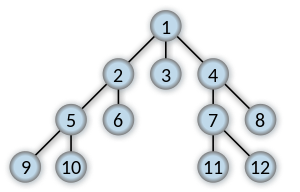
Breadth first search
|
Order in which the nodes are expanded
|
|
| Class | Search algorithm |
|---|---|
| Data structure | Graph |
| Worst-case performance | |
| Worst-case space complexity | |
Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key') and explores the neighbor nodes first, before moving to the next level neighbors.
BFS was invented in the late 1950s by E. F. Moore, who used it to find the shortest path out of a maze, and discovered independently by C. Y. Lee as a wire routing algorithm (published 1961).
Input: A graph Graph and a starting vertex root of Graph
Output: Goal state. The parent links trace the shortest path back to root
A non-recursive implementation of breadth-first search:
This non-recursive implementation is similar to the non-recursive implementation of depth-first search, but differs from it in two ways:
The Q queue contains the frontier along which the algorithm is currently searching.
The S set is used to track which vertices have been visited (required for a general graph search, but not for a tree search). At the beginning of the algorithm, the set is empty. At the end of the algorithm, it contains all vertices with a distance from root less than the goal.
The parent attribute of each vertex is useful for accessing the nodes in a shortest path, for example by backtracking from the destination node up to the starting node, once the BFS has been run, and the predecessors nodes have been set.
The NIL is just a symbol that represents the absence of something, in this case it represents the absence of a parent (or predecessor) node; sometimes instead of the word NIL, words such as null, none or nothing can also be used.
Note that the word node is usually interchangeable with the word vertex.
Breadth-first search produces a so-called breadth first tree. You can see how a breadth first tree looks in the following example.
...
Wikipedia