Bilunabirotunda
| Bilunabirotunda | |
|---|---|
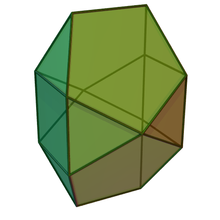 |
|
| Type |
Johnson J90 - J91 - J92 |
| Faces | 2x4 triangles 2 squares 4 pentagons |
| Edges | 26 |
| Vertices | 14 |
| Vertex configuration | 4(3.52) 8(3.4.3.5) 2(3.5.3.5) |
| Symmetry group | D2h |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
 |
|
In geometry, the bilunabirotunda is one of the Johnson solids (J91).
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
It is one of the elementary Johnson solids, which do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. However, it does have a strong relationship to the icosidodecahedron, an Archimedean solid. Either one of the two clusters of two pentagons and two triangles can be aligned with a congruent patch of faces on the icosidodecahedron. If two bilunabirotundae are aligned this way on opposite sides of the icosidodecahedron, then two vertices from the bilunabirotundae will meet in the very center of the icosidodecahedron.
The other two clusters of faces of the bilunabirotunda, each with one square and two triangles, can be aligned with a congruent patch of faces on the rhombicosidodecahedron. If two bilunabirotundae are aligned this way on opposite sides of the rhombicosidodecahedron, then a cube can be put between the bilunabirotundae at the very center of the rhombicosidodecahedron.
The following define the vertices of a bilunabirotunda centered at the origin with edge length 1:
where is the golden ratio.
...
Wikipedia

