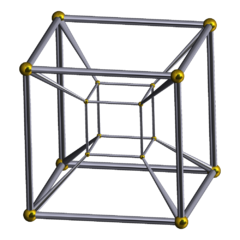
8-cell
| Tesseract 8-cell 4-cube |
|
|---|---|
|
|
| Type | Convex regular 4-polytope |
| Schläfli symbol | {4,3,3} t0,3{4,3,2} or {4,3}×{ } t0,2{4,2,4} or {4}×{4} t0,2,3{4,2,2} or {4}×{ }×{ } t0,1,2,3{2,2,2} or { }×{ }×{ }×{ } |
| Coxeter diagram |
|
| Cells | 8 (4.4.4) |
| Faces | 24 {4} |
| Edges | 32 |
| Vertices | 16 |
| Vertex figure |
 Tetrahedron |
| Petrie polygon | octagon |
| Coxeter group | B4, [3,3,4] |
| Dual | 16-cell |
| Properties | convex, isogonal, isotoxal, isohedral |
| Uniform index | 10 |
In geometry, the tesseract is the four-dimensional analog of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.
The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid,cubic prism, and tetracube (although this last term can also mean a polycube made of four cubes). It is the four-dimensional hypercube, or 4-cube as a part of the dimensional family of hypercubes or "measure polytopes".
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek τέσσερεις ακτίνες (téssereis aktines, "four rays"), referring to the four lines from each vertex to other vertices. In this publication, as well as some of Hinton's later work, the word was occasionally spelled "tessaract".
The tesseract can be constructed in a number of ways. As a regular polytope with three cubes folded together around every edge, it has Schläfli symbol {4,3,3} with hyperoctahedral symmetry of order 384. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }, with symmetry order 96. As a 4-4 duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}×{4}, with symmetry order 64. As an orthotope it can be represented by composite Schläfli symbol { } × { } × { } × { } or { }4, with symmetry order 16.
...
Wikipedia
