2-gon

Regular digon
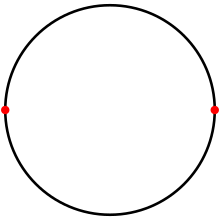
On a circle, a digon is a tessellation with two antipodal points, and two 180° arc edges.
Type	Regular polygon
Edges and vertices	2
Schläfli symbol	{2}
Coxeter diagram
Symmetry group	D2, [2], (*2•)
Dual polygon	Self-dual

In geometry, a digon is a polygon with two sides (edges) and two vertices. Its construction is degenerate in a Euclidean plane because either the two sides would coincide or one or both would have to be curved.

A regular digon has both angles equal and both sides equal and is represented by Schläfli symbol {2}. It may be constructed on a sphere as a pair of 180 degree arcs connecting antipodal points, when it forms a lune.

The digon is the simplest abstract polytope of rank 2.

A truncated digon, t{2} is a square, {4}. An alternated digon, h{2} is a monogon, {1}.

A straight-sided digon is regular even though it is degenerate, because its two edges are the same length and its two angles are equal (both being zero degrees). As such, the regular digon is a constructible polygon.

Some definitions of a polygon do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case.

A digon as a face of a polyhedron is degenerate because it is a degenerate polygon. But sometimes it can have a useful topological existence in transforming polyhedra.

A spherical lune is a digon whose two vertices are antipodal points on the sphere.